Molecular Dynamics Simulation
An introduction to soft-particle Molecular Dynamics (MD) simulation. This file is also a working MD simulator. A companion file introMDpbc.m is also available with fewer comments.
- [ MDIntro.pdf ] pdf version.
- [ MDIntro.php ] html version.
Contents
- Theory I: Solving Newtons Laws for collection of particles
- Figure 1: Diagram defining particle-particle interaction variables.
- Simple Molecular Dynamics Simulation
- Experimental Parameters (particle)
- Experimental Parameters (space-domain)
- Experimental Parameters (initial conditions)
- Experimental Parameters (time-domain)
- Display Parameters
- Theory II: Numeric integration of Newton's laws Part I
- Figure 2: Euler vs. Semi-implicit Euler Integration.
- Theory II: Numeric integration of Newton's laws Part II
- Figure 3: Velocity Verlet vs. Semi-implicit Euler Integration.
- Figure 3: Velocity Verlet vs. Semi-implicit Euler Integration (caption).
- Simulation Parameters
- Initial Conditions (Positions)
- Initial Conditions (Velocities)
- Initial Conditions (Accelerations)
- Save variables
- Figure 3: Setup Plotting
- Main Loop
- m-files
Theory I: Solving Newtons Laws for collection of particles
A Molecular Dynamics (MD) simulation is a computer simulation of Newton's Laws for a collection of 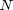 particles. The
particles. The  -th particle at initial position
-th particle at initial position 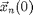 with velocity
with velocity 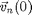 moves according to Newton's Law:
moves according to Newton's Law:
![$$M_n\frac{d^2}{d t^2}\vec{x}_n(t)=\vec{F}_{n}(t)=
\sum_{m=1}^N \vec{F}_{nm}(t)+\vec{F}_n^e(t),\;\;\;\;\;\;[1]$$](MDIntro_eq50232.png)
where 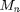 is the mass of particle
is the mass of particle  ,
, 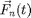 is the force on particle
is the force on particle  ,
, 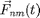 is the force on particle
is the force on particle  from particle
from particle  , and
, and 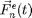 is the sum of all external forces. For this introduction, we assume that the force is obtained from a scalar potential
is the sum of all external forces. For this introduction, we assume that the force is obtained from a scalar potential 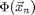 such that
such that
![$$
\vec{F}_{nm}=
-\frac{\partial}{\partial\vec{x}_n}
\Phi(\vec{x}_m,\vec{x}_n).
\;\;\;\;\;\;[2]
$$](MDIntro_eq43152.png)
Figure 1: Diagram defining particle-particle interaction variables.
MDfigures(1);
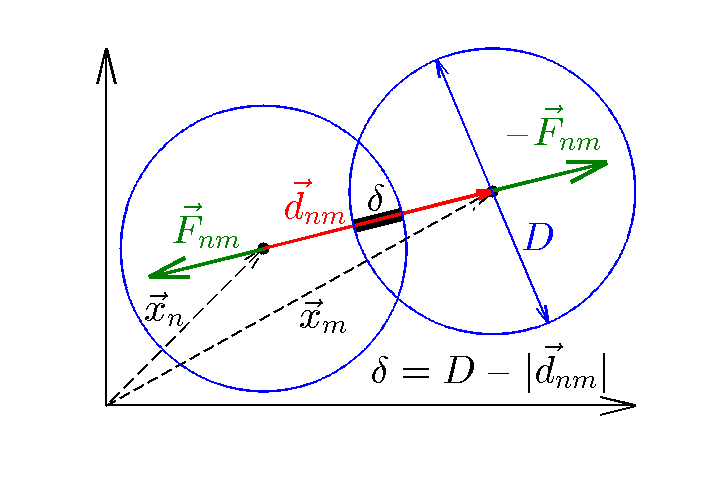
We will further assume the particles are disks with a simple harmonic potential:
![$$
\Phi(\vec{x}_m,\vec{x}_n) =
\Phi(|\vec{x}_m-\vec{x}_n|) =
\Phi(d_{nm})=\frac{1}{2}K(D-d_{nm})^2=\frac{1}{2}K\delta^2,
\;\;\;\;\;\;[3a]
$$](MDIntro_eq26464.png)
where
![$$
\vec{d}_{nm}=\vec{x}_m-\vec{x}_n
\;\;\;\;\;\;[3b]
$$](MDIntro_eq87202.png)
is the vector pointing from the center of particle  to the center of particle
to the center of particle  and
and
![$$
d_{nm}=|\vec{d}_{nm}|;
\;\;\;\;\;\;[3c]
$$](MDIntro_eq83305.png)
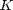 is a material constant that determines how hard the material is,
is a material constant that determines how hard the material is, 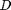 is the particle diameter, and
is the particle diameter, and
![$$
\delta=D-|\vec{d}_{nm}|
\;\;\;\;\;\;[3d]
$$](MDIntro_eq25229.png)
is the particle overlap. (See Figure 1.) Differentiating the potential, the force
![$$
\vec{F}_{nm}=-K \delta\hat{d}_{nm}.
\;\;\;\;\;\;[3e]
$$](MDIntro_eq56272.png)
The direction of the force is opposite to the unit vector 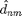 pointing from particle
pointing from particle  to
to  , which pushes the particles apart. From Newton's third law the force on particle
, which pushes the particles apart. From Newton's third law the force on particle  from
from  is
is
![$$
\vec{F}_{mn}=-\vec{F}_{nm}.
\;\;\;\;\;\;[3f]
$$](MDIntro_eq99403.png)
In this introduction we use a contact force, which only acts when the particles are in contact. That is, the force is zero if
![$$
\delta<=0.
\;\;\;\;\;\;[3g]
$$](MDIntro_eq15708.png)
Simple Molecular Dynamics Simulation
introMDpbc.m contains the same code without the explanation:
Experimental Parameters (particle)
Here we define all of the particle parameters needed to determine the forces between particle pairs:
N=80; % number of particles D=2; % diameter of particles K=100; % force vector n<-m Fnm=-K*(D/|dnm|-1)*dnm, where vect dnm=Xm-Xn M=3; % mass of particles
Experimental Parameters (space-domain)
This simulation uses a periodic domain. In a periodic domain there are copies or images of each particle separated by 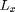 and
and 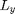 such that for each particle a positions
such that for each particle a positions 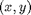 there are also particles at
there are also particles at
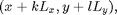
for all integers  and
and  . In the main simulation box
. In the main simulation box 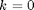 and
and  . For this simulation we need the distance between all particle pairs, but since we have a short range potential [3g] we only need the nearest image distance. This calculation is done below in the main loop.
. For this simulation we need the distance between all particle pairs, but since we have a short range potential [3g] we only need the nearest image distance. This calculation is done below in the main loop.
Here we define parameters needed to determine the space-domain for the particles in a periodic box of size Lx by Ly.
Lx=10*D; % size of box
Ly=10*D;
Experimental Parameters (initial conditions)
We choose random velocities with the property that the total kinetic energy: M/2*sum(vx.^2+vy.^2)=KEset.
KEset=5; % initial total Kinetic Energy (KE)
Experimental Parameters (time-domain)
The time-domain is from 0 to TT.
TT=1; % total simulation time (short for demo).
Display Parameters
This section controls the simulation plotting animation
demo=true; % true for this demo plotit=false; % plot ? off for this demo Nplotskip=50; % number of time steps to skip before plotting
Theory II: Numeric integration of Newton's laws Part I
To solve [1] we first rewrite it as two first-order equations:
![$$
\begin{array}{lcl}
\displaystyle
\frac{d}{dt}\vec{x}_n(t) & = & \vec{v}_n(t).\\[13pt]
\displaystyle
\frac{d}{dt}\vec{v}_n(t) & = & \vec{F}_n(t)/M_n.\\
\end{array}
\;\;\;\;\;\;[4]
$$](MDIntro_eq53183.png)
When solving [4] numerically, time is broken up into discrete steps of size 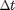 (i.e.,
(i.e., 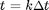 , where k is an integer). If
, where k is an integer). If 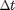 is small we can approximate [4] with:
is small we can approximate [4] with:
![$$
\begin{array}{lcl}
\left[
\vec{x}_n\left( (k+1)\Delta t \right)
-\vec{x}_n(k\Delta t)
\right]/\Delta t & \simeq & \vec{v}_n(k\Delta t).\\[10pt]
\left[
\vec{v}_n\left( (k+1)\Delta t \right)
-\vec{v}_n(k\Delta t)
\right]/\Delta t & \simeq & \vec{F}_n(t)/M_n.\\
\end{array}
\;\;\;\;\;\;[5]
$$](MDIntro_eq55265.png)
Solving for the later times 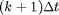 in terms of earlier times
in terms of earlier times  :
:
![$$
\begin{array}{lclcl}
\vec{x}_n^{(k+1)} & \equiv & \vec{x}_n\left( (k+1)\Delta t \right)
& \simeq & \vec{x}_n^{(k)}+\vec{v}_n^{(k)}\Delta t\\[10pt]
\vec{v}_n^{(k+1)} & \equiv & \vec{v}_n\left( (k+1)\Delta t \right)
& \simeq & \vec{v}_n^{(k)}+\vec{F}_n^{(k)}/M_n\Delta t\\
\end{array}
\;\;\;\;\;\;[6]
$$](MDIntro_eq48250.png)
Equation [6] discovered by L. Euler is called the Euler Method and could be used to integrate the system to get the new positions 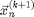 and velocities
and velocities 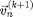 from the old positions
from the old positions 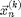 , velocities
, velocities 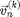 , and forces
, and forces 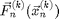 , which only depends on
, which only depends on 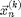 . However [6] is not recommended. If we use [6] the energy of the system will grow without bounds as seen in Figure 2. To make a useful integration scheme we can change the order of integration. If we calculate
. However [6] is not recommended. If we use [6] the energy of the system will grow without bounds as seen in Figure 2. To make a useful integration scheme we can change the order of integration. If we calculate 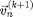 first we can use it to calculate
first we can use it to calculate 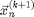 . These equation are an enhanced version of Euler's method called the Semi-implicit Euler Method:
. These equation are an enhanced version of Euler's method called the Semi-implicit Euler Method:
![$$
\begin{array}{lcl}
\vec{v}_n^{(k+1)} &\simeq&
\vec{v}_n^{(k)}+\vec{F}_n^{(k)}/M_n\Delta t.\\[10pt]
\vec{x}_n^{(k+1)} &\simeq&
\vec{x}_n^{(k)}+\vec{v}_n^{(k+1)}\Delta t.\\
\end{array}
\;\;\;\;\;\;[7]
$$](MDIntro_eq73930.png)
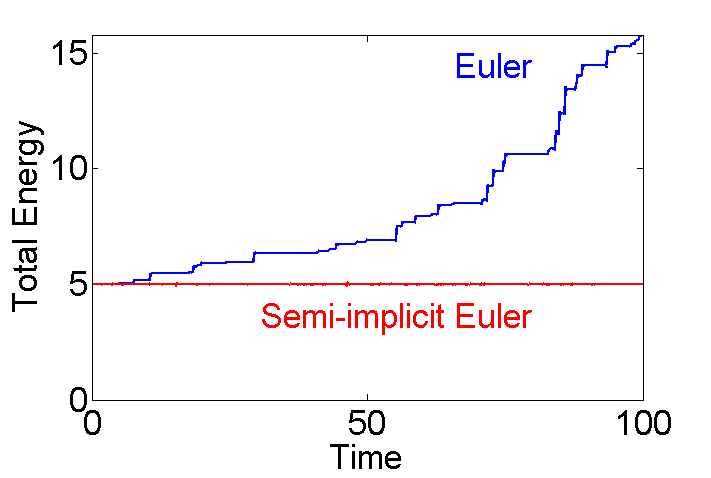
Figure 2 compares an Euler simulation from eulerMDpbc.m with an semi-implicit Euler simulation from eEulerMDpbc.m. The semi-implicit Euler method is the simplest example of a general method called Symplectic Integration, which is designed to conserve energy.
Figure 2: Euler vs. Semi-implicit Euler Integration.
The following code is used to produce figure 2. External files eulerMDpbc.m and eEulerMDpbc.m are used.
KE=5; % initial Kinetic Energy Ts=100; % total simulation time [Ek Ep]=eulerMDpbc(10,KE,Ts,false); % 10 particle--Euler integration eTe=Ek+Ep; % save total energy for Euler; [Ek Ep]=eEulerMDpbc(10,KE,Ts,false); % 10 particle--Semi-implicit Euler eTse=Ek+Ep; % save total energy for semi-implicit Euler Nt=length(Ek); % number of time steps t=(0:Nt-1)/Nt*Ts; % simulation time fs=25; plot(t,eTe,t,eTse,'r','linewidth',2); % plot total energy axis([0 Ts 0 inf]); set(gca,'fontsize',fs); xlabel('Time'); ylabel('Total Energy'); text(80,eTe(fix(90/Ts*Nt)),'Euler',... 'color','b','fontsize',fs,'horizontal','right'); text(80,.9*KE,'Semi-implicit Euler',... 'color','r','fontsize',fs,... 'horizontal','right','vertical','top');
Theory II: Numeric integration of Newton's laws Part II
It is clear that energy conservation is poor using the (blue) Euler method. In principle Equation [7] could be used for simple MD simulations. However, both methods are only accurate to first order in 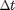 , and this limits the usefulness of the semi-implicit Euler method.
, and this limits the usefulness of the semi-implicit Euler method.
In this introduction we use a Symplectic Integrator with errors proportional to 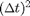 and good energy conservation due to L. Verlet called Velocity Verlet integration. The main drawback of the semi-implicit Euler method the error is proportional to
and good energy conservation due to L. Verlet called Velocity Verlet integration. The main drawback of the semi-implicit Euler method the error is proportional to 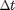 . Since we used dt=0.01, we can expect errors of order 1% (see Figure 3). Sometimes that is not sufficient. One option is to decrease dt, but the drawback is that the simulation time is increase proportionally. So with dt=0.01/100=0.0001 semi-implicit Euler would give error of order 0.01% the simulation time would increase by a factor of 100. To overcome this deficiency Verlet devised a different integration scheme based on a second order approximation to [4] as follows:
. Since we used dt=0.01, we can expect errors of order 1% (see Figure 3). Sometimes that is not sufficient. One option is to decrease dt, but the drawback is that the simulation time is increase proportionally. So with dt=0.01/100=0.0001 semi-implicit Euler would give error of order 0.01% the simulation time would increase by a factor of 100. To overcome this deficiency Verlet devised a different integration scheme based on a second order approximation to [4] as follows:
![$$
\begin{array}{lcll}
\vec{x}_n^{(k+1)}
&\simeq&
\vec{x}_n^{(k)}+
\vec{v}_n^{(k)}\Delta t+
\frac{1}{2}\vec{a}_n^{(k)}(\Delta t)^2.
&\;\;\;\;\;\;[8]\\[10pt]
\displaystyle
\vec{a}_n^{(k+1)}
&=&
\displaystyle
\frac{1}{M_n}\sum_{m=1}^N
\vec{F}_{nm}(|\vec{x}_m^{(k+1)}-\vec{x}_n^{(k+1)}|)
&\;\;\;\;\;\;[9]\\[20pt]
\vec{v}_n^{(k+1)}
&\simeq& \vec{v}_n^{(k)}+
\frac{1}{2}(\vec{a}_n^{(k+1)}+\vec{a}_n^{(k)})\Delta t.
&\;\;\;\;\;\;[10]\\
\end{array}$$](MDIntro_eq43465.png)
Figure 3: Velocity Verlet vs. Semi-implicit Euler Integration.
The following code is used to produce figure 3. External files verletMDpbc.m and eEulerMDpbc.m are used.
KE=5; % initial Kinetic Energy Ts=100; % total simulation time [Ek Ep]=verletMDpbc(10,KE,Ts,false); % 10 particle--Verlet integration eTv=Ek+Ep; % save total energy for Verlet; Nt=length(Ek); % number of time steps t=(0:Nt-1)/Nt*Ts; % simulation time fs=25; plot(t,eTv,t,eTse,'r','linewidth',2); % plot total energy hold on; plot(t,[0*t+1.01*KE;0*t+.99*KE],'r--','linewidth',2); % 1% error plot([73 85],[1.014 1]*KE,'linewidth',2); hold off; axis([0 Ts 5*(1+[-.02 .0201])]); set(gca,'fontsize',fs); xlabel('Time'); ylabel('Total Energy'); text(50,1.014*KE,'Velocity Verlet',... 'color','b','fontsize',fs,'horizontal','center'); text(50,.988*KE,'Semi-implicit Euler \pm 1%',... 'color','r','fontsize',fs,... 'horizontal','center','vertical','top');
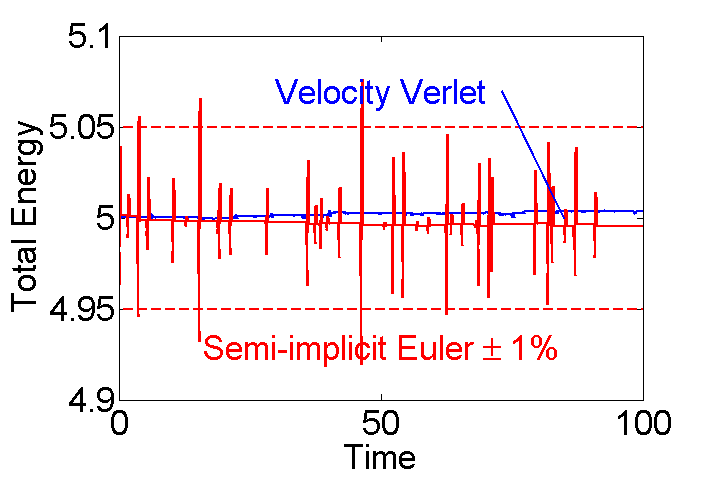
Figure 3: Velocity Verlet vs. Semi-implicit Euler Integration (caption).
Figure 3 shows the total energy over time for a 10 particle system using the Semi-implicit Euler integration method from [7] (red) and Velocity Verlet from [8-10] (blue). Red dashed lines show a range of 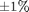 . The error for the Velocity Verlet is
. The error for the Velocity Verlet is 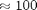 times smaller.
times smaller.
Simulation Parameters
Regardless of the integration method 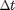 (dt in code) must be determined. Here we use a fixed time step dt=0.01
(dt in code) must be determined. Here we use a fixed time step dt=0.01 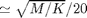 . The total number of time steps Nt is determined from the total simulation time TT.
. The total number of time steps Nt is determined from the total simulation time TT.
dt=1e-2; % integration time step Nt=fix(TT/dt); % number of time steps
Initial Conditions (Positions)
The particles need to be placed in the box with minimal overlap to avoid excess potential energy at the beginning of the simulation. For moderately dense systems a square grid can be used. The matlab command ndgrid creates D spaced points on a grid inside of the Lx by Ly box. randperm randomly chooses N positions from all numel(x) available locations. The final result is a pair of matlab vectors x and y each with size(x)=[1,N] that represents 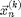 at each time
at each time  . Here, for the initial conditions before the simulation starts
. Here, for the initial conditions before the simulation starts 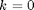 . In the code
. In the code  is represented in matlab as nt, the time step number.
is represented in matlab as nt, the time step number.
[x y]=ndgrid(D/2:D:Lx-D/2,D/2:D:Ly-D/2); % place particles on grid ii=randperm(numel(x),N); % N random position on grid x=x(ii); % set x-positions y=y(ii); % set y-positions
Initial Conditions (Velocities)
The velocities vx and vy each with size(vx)=[1,N] represent 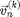 at time
at time  . Here, for the initial conditions before the simulation starts
. Here, for the initial conditions before the simulation starts 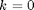 . The velocities are chosen randomly from a normal distribution using randn. The mean velocity is removed to avoid center of mass drift. The variance of the distribution is set so that the total kinetic energy: M/2*sum(vx.^2+vy.^2)=KEset.
. The velocities are chosen randomly from a normal distribution using randn. The mean velocity is removed to avoid center of mass drift. The variance of the distribution is set so that the total kinetic energy: M/2*sum(vx.^2+vy.^2)=KEset.
vx=randn(1,N)/3; % normal (Maxwell) distribution of velocities vy=randn(1,N)/3; vx=vx-mean(vx); % remove center of mass drift vy=vy-mean(vy); tmp=sqrt(2*KEset/M/sum((vx.^2+vy.^2))); % set Kinetic energy vx=vx*tmp; vy=vy*tmp;
Initial Conditions (Accelerations)
The accelerations from the  previous time step is need for Verlet's second order integration scheme.
previous time step is need for Verlet's second order integration scheme.
ax_old=0*x; % need initial condition for velocity Verlet integration
ay_old=0*y;
Save variables
List of quantities to be saved at each time step.
Ek=zeros(Nt,1); % Kinetic Energy Ep=zeros(Nt,1); % particle-particle potential xs=zeros(Nt,N); % x-position ys=zeros(Nt,N); % y-position vxs=zeros(Nt,N); % x-velocity vys=zeros(Nt,N); % y-velocity
Figure 3: Setup Plotting
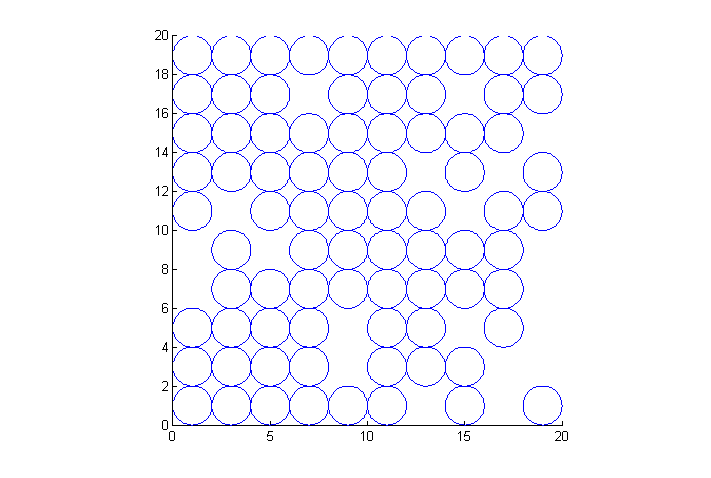
Here we use an external function plotNCirc.m to create an animation of the simulations progress. plotNCirc returns an array of handles h to a rectangle object for each of the N particles. Matlab rectangles contain a curvature property with turns them into circles. The handles are used later to animate the particle positions. An example initial condition is shown here.
NB: periodic images of particles are not shown
if(plotit || demo) % only if plotit true clf; % clear figure h=plotNCirc(x,y,D,'none'); % plot particles no color; store handle h axis('equal'); % square pixels axis([0 Lx 0 Ly]); % piloting range end
Main Loop
In the main loop the simulation steps through Nt time steps, advancing time, the particle positions, forces, and velocities. Comments refer back to sections and equations above.
for nt=1:Nt % plot particles if(plotit && rem(nt-1,Nplotskip+1)==0) % nt-1 divides Nplotskip+1 xp=mod(x,Lx); yp=mod(y,Ly); for np=1:N set(h(np),'Position',[xp(np)-.5*D yp(np)-.5*D D D]); % update handle end drawnow; end x=x+vx*dt+ax_old*dt^2/2; % first step in Verlet integration eq.[8] y=y+vy*dt+ay_old*dt^2/2; % position dependent calculations xs(nt,:)=x; % save positions ys(nt,:)=y; % Force between particles eq. [9] and [3a-g] Fx=zeros(1,N); % zero forces Fy=zeros(1,N); for nn=1:N % check particle n for mm=nn+1:N % against particle m from n+1->N dy=y(mm)-y(nn); % [3b] y-comp dnm vector from from n->m dy=dy-round(dy/Ly)*Ly; % closest periodic image if(abs(dy)<D) % [3g] y-distance close enough? dx=x(mm)-x(nn); % [3b] x-comp dnm vector from from n->m dx=dx-round(dx/Lx)*Lx; % closest periodic image dnm=dx.^2+dy.^2; % [3c] squared distance between n and m if(dnm<D^2) % [3g] overlapping? dnm=sqrt(dnm); % [3c] distance F=-K*(D/dnm-1); % [3d-e] force magnitude Fx(nn)=Fx(nn)+F.*dx; % [9,3e] accumulate x force on n Fx(mm)=Fx(mm)-F.*dx; % [9,3ef] x force on m (equal opposite) Fy(nn)=Fy(nn)+F.*dy; % [9,3e] accumulate y force on n Fy(mm)=Fy(mm)-F.*dy; % [9,3ef] y force on m (equal opposite) Ep(nt)=Ep(nt)+(D-dnm).^2;% [3a] particle-particle potential I end end end end Ep(nt)=K/2*Ep(nt); % eq [3a] particle particle potential II ax=Fx./M; % eq [9] calc a from F=Ma ay=Fy./M; vx=vx+(ax_old+ax)*dt/2; % eq [10] second step in Verlet integration vy=vy+(ay_old+ay)*dt/2; % velocity dependent calculations Ek(nt)=M*sum((vx.^2+vy.^2))/2; % Kinetic energy vxs(nt,:)=vx; % save velocities vys(nt,:)=vy; ax_old=ax; % need for eqs [8-10] save for next step ay_old=ay; end
m-files
- MDIntro.zip All files in one zip file.
- MDIntro.m Introduction to Molecular dynamics (This File).
- MDIntro.pdf (pdf version).
- introMDpbc.m Version of this file without discussion.
- introMDwalls.m Version with walls instead of periodic boundaries.
- eulerMDpbc.m Function to demonstrate Euler Integration.
- eEulerMDpbc.m Function to demonstrate Semi-implicit Euler Integration.
- verletMDpbc.m Function to demonstrate Velocity Verlet Integration.
- MDfigures.m Create figures.
- plotNCirc.m Plot N circles and return handles.
